Answer:
Number of child tickets = 800
Number of adult tickets = 330
Explanation:
Let c = number of child tickets
and a= the number of adult tickets.
We are given:
The admission fee at the steamboat springs hot air balloon festival is $1.50 for children and $4.00 for adults.
On a certain day, 1,130 enter the festival and 2, 520 is collected.
Making equations:
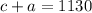 (because total people entered are 1130, so adding number of adult and child tickets will give us total number of people)
(because total people entered are 1130, so adding number of adult and child tickets will give us total number of people)
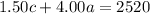 (because total money collected is 2520, so adding coat of adult and child tickets will give us total money)
(because total money collected is 2520, so adding coat of adult and child tickets will give us total money)
Now, solving these equations simultaneously, we can find values of x and y
Let:
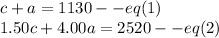
From equation 1 find value of c and put it in eq(2)
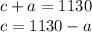
Putting value of c in eq(2)
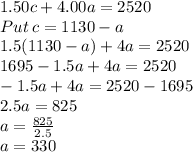
So, we get value of a = 330
Now, punting value of a in eq(1) to get value of c
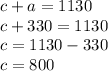
So, we get value of c = 800
Therefore:
Number of child tickets = c= 800
Number of adult tickets = a = 330