Answer:
These equations describe two lines that intersect at the point (-1, 8), one of them with a slope of 3, the other with a slope of -4.
Explanation:
We can find the point where these two lines intersect by taking one of the equations, solving it for x, and substituting it into the other equation.
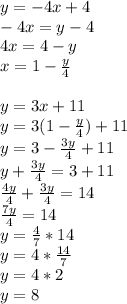
Now we can plug that into our first equation to find x
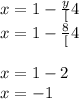
So these lines intersect at the point (-1, 8), one of them with a slope of 3, the other with a slope of -4