Please find the derivative of x3^((2x^2-1)). Show all of your work and explain as much as possible.

Question

Please find the derivative of
`x3^((2x^2-1))`. Show all of your work and explain as much as possible.

Answer 1

`3^(2x^2-1)+4ln(3)*3^(2x^2-1)x^2`

Explanation:

`x3^((2x^2-1))`

~Apply product rules

`(d)/(dx)(x)3^(2x^2-1)+(d)/(dx)(3x^(2x^2-1))x\\(d)/(dx)=1\\(3^(2x^2-1))=4ln(3)*3x^(2x^2-1)x\\1*3^(2x^2-1)+4ln(3)*3^(2x^2-1)xx`

~Simplify

`3^(2x^2-1)+4ln(3)*3^(2x^2-1)x^2`

Best of Luck!

Answer 2

Hello! :)

`\large\boxed{(dy)/(dx) = 3^{(2x^(2) - 1)} (4x^(2)ln3 + 1)}`

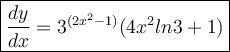
Use the Product Rule to solve for the derivative:

`(dy)/(dx)= f(x) * g'(x) + g(x) * f'(x)`

We can divide the expression into two different functions:

`f(x) = x\\\\g(x) = 3^{2x^(2) -1}`

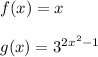
Use the Product Rule equation and the following rules to solve for the derivative:

Derivative of an exponential function with base other than e:

`(dy)/(dx) a^(u) = a^(u) * u' * lna`

Power rule:

`(dy)/(dx) x^(n) = nx^((n-1))`

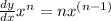
Find the derivatives using the power rule and derivative of an exponential function. Plug these into the product rule equation:

`(dy)/(dx) = x(3^{(2x^(2) -1)} * 4x* ln3) + (1)3^{(2x^(2) - 1)}`

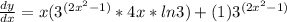
Simplify by factoring out a common factor:
`3^{(2x^(2) - 1)}`

`(dy)/(dx) = 3^{(2x^(2) - 1)}( x* 4x * ln3) + (1)`

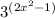
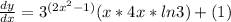
Simplify further:

`(dy)/(dx) = 3^{(2x^(2) - 1)} (4x^(2)ln3 + 1)`

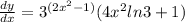
This is the final derivative.