Answer:
D.
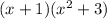
Explanation:
Hello!
We can group the first two terms and the last two terms.
Factor by Grouping
Factoring by grouping is the process of breaking down larger polynomials to smaller ones to factor. We can then combine like factors.
In the second step, we can see that we can rewrite
 as
as
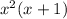 , as both the two terms share a common factor of
, as both the two terms share a common factor of
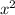 . We can pull out
. We can pull out
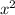 from that expression. Similarly,
from that expression. Similarly,
 and
and
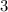 share a common factor of
share a common factor of
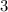 , so we can pull that out.
, so we can pull that out.