Answer:
The equation of the polynomial in vertex form is
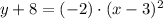 , its vertex is
, its vertex is
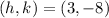 .
.
The expression of the axis of symmetry is
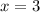 .
.
The y-intercept of the function is -26.
Explanation:
The vertex form of the second order polynomial is defined by the following expression:
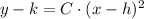 (1)
(1)
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
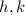 - Coordinates of the vertex, dimensionless.
- Coordinates of the vertex, dimensionless.
 - Vertex constant, dimensionless.
- Vertex constant, dimensionless.
Let
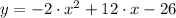 , then we proceed to present the produre for the determination of the vertex form:
, then we proceed to present the produre for the determination of the vertex form:
1)
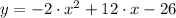 Given
Given
2)
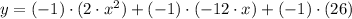
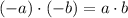 /
/
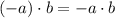
3)
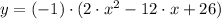 Distributive property
Distributive property
4)
![y = [(-1)\cdot (2)]\cdot (x^(2)-6\cdot x +13)](https://img.qammunity.org/2021/formulas/mathematics/college/dxecf716t2h4afww5drsv4g4uqxpr2s1az.png) Associative and distributive properties
Associative and distributive properties
5)
![y = (-2)\cdot [(x^(2)-6\cdot x+9)+4]](https://img.qammunity.org/2021/formulas/mathematics/college/nrdrljudoo6bgs2isvik90x75tb94pymoi.png)
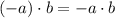
6)
![y = (-2) \cdot [(x-3)^(2)+4]](https://img.qammunity.org/2021/formulas/mathematics/college/8jit1moary8pq20bs6a8ck4xbdui61w51y.png) Perfect square trinomial
Perfect square trinomial
7)
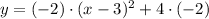 Distributive property
Distributive property
8)
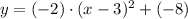
9)
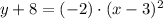 Compatibility of addition/Existence of the additive inverse/Modulative property/Result.
Compatibility of addition/Existence of the additive inverse/Modulative property/Result.
The equation of the polynomial in vertex form is
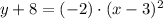 , its vertex is
, its vertex is
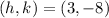 .
.
The axis of symmetry is a line perpendicular to axis in which the square component of the vertex form is set. The expression of the axis of symmetry is
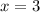 .
.
The y-intercept is the value of the polynomial when
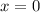 , then, the value is:
, then, the value is:

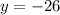
The y-intercept of the function is -26.