Question

Verify the following reduction formula:


`\displaystyle \int \sec^n(u)\, du=(\sec^(n-2)(u)\tan(u))/(n-1)+(n-2)/(n-1)\int \sec^(n-2)(u)\, du, \; n\\eq 1`

Answer 1

See Explanation.

General Formulas and Concepts:

Pre-Algebra

• Distributive Property
• Equality Properties

Algebra I

• Combining Like Terms

Algebra II

• Exponential Rules

Pre-Calculus

• Pythagorean Identities: tan²(x) = sec²(x) - 1

Calculus

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Integration Rule 1:
`\int {cf(x)} \, dx = c\int {f(x)} \, dx`

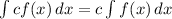
Integration Rule 2:
`\int {f(x) \pm g(x)} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

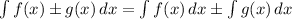
Integration 1:
`\int {sec^2(u)} \, du = tan(u) + C`

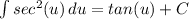
Integration by Parts:
`\int {u} \, dv = uv - \int {v} \, du`

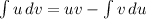
• [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig

Explanation:

Step 1: Define

`\int {sec^n(u)} \, du`

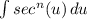
Step 2: Rewrite

1. [Integral - Alg] Separate Exponents:
   `\int {sec^n(u)} \, du = \int {sec^(n-2)(u)sec^2(u)} \, du`

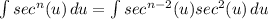
Step 3: Identify Variables

Using LIPET, we define variables to use IBP.

Use Integration 1.

`u = [sec(u)]^(n-2) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = sec^2(u)du\\du = (n-2)[sec(u)]^(n-3) sec(u)tan(u) \ \ \ \ \ \ \ \ v = tan(u)`

Step 4: Integrate

1. Integrate [IBP]:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - \int [{tan(u)(n-2)[sec(u)]^(n-3)sec(u)tan(u)} ]\, du`
2. [Integral - Alg] Multiply:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - \int [{tan^2(u)(n-2)[sec(u)]^(n-2)}] \, du`
3. [integral - Int Rule 1] Simplify:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - (n-2)\int [{tan^2(u)[sec(u)]^(n-2)}] \, du`
4. [Integral - Pythagorean Identities] Rewrite:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - (n-2)\int [{[sec^2(u) - 1][sec(u)]^(n-2)}] \, du`
5. [Integral - Alg] Multiply/Distribute:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - (n-2)\int [{sec^n(u)-[sec(u)]^(n-2)}] \, du`
6. [Integral - Int Rule 2] Rewrite:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - (n-2) [\int {sec^n(u)} \, du - \int {[sec(u)]^(n-2)} \, du ]`
7. [Integral - Alg] Distribute:
   `\int {sec^n(u)} \, du = tan(u)[sec(u)]^(n-2) - (n-2) \int {sec^n(u)} \, du + (n-2)\int {[sec(u)]^(n-2)} \, du`
8. Rewrite:
   `\int {sec^n(u)} \, du = sec^(n-2)(u)tan(u) - (n-2) \int {sec^n(u)} \, du + (n-2)\int {[sec(u)]^(n-2)} \, du`
9. [Integral - Alg] Isolate Integral Term:
   `\int {sec^n(u)} \, du + (n-2) \int {sec^n(u)} \, du = sec^(n-2)(u)tan(u) + (n-2)\int {[sec(u)]^(n-2)} \, du`
10. [Integral - Alg] Combine Like Terms:
    `(n - 1)\int {sec^n(u)} \, du = sec^(n-2)(u)tan(u) + (n-2)\int {[sec(u)]^(n-2)} \, du`
11. [Integral 2 - Alg] Rewrite:
    `(n - 1)\int {sec^n(u)} \, du = sec^(n-2)(u)tan(u) + (n-2)\int {sec^(n-2)(u)} \, du`
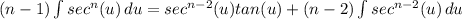
12. [Integral - Alg] Isolate Original Integral:
    `\int {sec^n(u)} \, du = (sec^(n-2)(u)tan(u))/(n-1) + (n-2)/(n-1) \int {sec^(n-2)(u)} \, du`

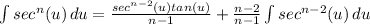
And we have proved the Reduction Formula!