Question

Solve the inequality. Graph the solution.

−8≤z+6.4
The solution is

Answer 1

Solve the inequality. Graph the solution.

−8≤z+6.4
The solution is

Answer 2

The solution to the inequality
`\( -8 \leq z + 6.4 \) is \( z \geq -14.4 \)`.

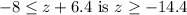Step-by-step explanation:

To solve the given inequality, we aim to isolate the variable
`\( z \)` on one side of the inequality. Here are the detailed steps:

Starting with the inequality
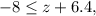`\( -8 \leq z + 6.4 \),` we want to get
`\( z \)` by itself.

1. Subtract 6.4 from both sides:

`\[ -8 - 6.4 \leq z \]`

`\[ -14.4 \leq z \]`

So, the solution is
`\( z \geq -14.4 \)`. This means that any value of
`\( z \)` greater than or equal to -14.4 satisfies the given inequality.

Now, let's consider the graphical representation on a number line. We mark a filled circle at -14.4 to indicate the inclusive endpoint, and we draw an arrow to the right, representing that the solution extends infinitely in that direction. This visual representation helps in understanding the range of values for
`\( z \)` that satisfy the inequality.