Points of Intersection
To find the point of intersection for two lines, we can use substitution to solve for the coordinates.
Solving the Question
We're given:
With these two equations, we can:
- First isolate x in the second equation
- Use substitution to input in second equation into the first and solve for y
- Use the y-coordinate to find the corresponding x-coordinate using substitution
Isolate x in the second equation:
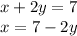
Substitute the second equation into the first:
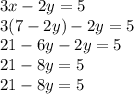
Solve for y:
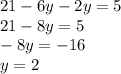
Solve for x:
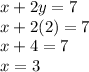
Answer
The point of intersection of the lines is (3,2).