Answer: Choice [D] - "power of a power" ✅
Explanation:
Hii, do you need to know which law you should use to simplify
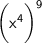 ?
?
No problem!
The law we will use here is "power of a power".
What "power of powers" means is we raise a power to a power, which is exactly what we do here: We raise x^4 to the power of 9. To simplify our expression, we multiply the powers. (
 )
)
So the right answer is: Choice [D] - "Power of a power"
The simplified answer is

Voila! There's our answer, cheers!
--
Hope that this helped! Best wishes.
--