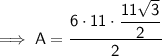Question

I keep putting in the formula but I keep getting the answer wrong​

Answer 1

314 in² (nearest whole number)

Explanation:

Radius of a regular polygon: The distance from the center of the polygon to any vertex. The radius of a hexagon is equal to the length of one side.

Therefore, from inspection of the given diagram:

• radius = 11 in ⇒ side length = 11 in

To find the area of a regular polygon, we first need to calculate the apothem. The apothem is the line drawn from the center of the polygon to the midpoint of one of its sides.

`\textsf{Length of apothem (a)}=(s)/(2 \tan\left((180^(\circ))/(n)\right))`

where:

• s = length of one side
• n = number of sides

Given:

• s = 11 in
• n = 6

Substitute the given values into the formula and solve for a:

`\implies \textsf{a}=(11)/(2 \tan\left((180^(\circ))/(6)\right))=(11√(3))/(2)`

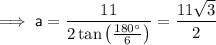
Area of a Regular Polygon

`\textsf{A}=(n\:s\:a)/(2)`

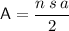
where:

• n = number of sides
• s = length of one side
• a = apothem

Given:

• n = 6
• s = 11

• 
  `\textsf{a}=(11√(3))/(2)`

Substitute the given values into the formula and solve for A:

`\implies \sf A=(6 \cdot 11 \cdot (11√(3))/(2))/(2)`

`\implies \sf A=314.3672216...`

`\implies \sf A=314\:\:in^2\:\:(nearest\:whole\:number)`