Answer:
Acceleration of this man: approximately
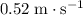 due east.
due east.
Accelerate of this woman: approximately
 due west.
due west.
Step-by-step explanation:
The question implies that the net force on the man is
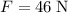 due east. The mass of the man is
due east. The mass of the man is
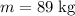 . The acceleration of the man would be:
. The acceleration of the man would be:
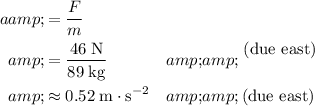 .
.
In other words, the acceleration of this man would be approximately
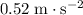 due east (same direction as the net force.)
due east (same direction as the net force.)
By Newton's Laws of Motion, for every force there is a reaction force that is equal in magnitude but opposite in direction.
The woman in this question is applying a due east
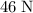 force on the man. Thus, this woman would experience a reaction force of the same magnitude (
force on the man. Thus, this woman would experience a reaction force of the same magnitude (
 ) and opposite direction (due west) from the man. Under assumptions of the question, the net force on the woman would be
) and opposite direction (due west) from the man. Under assumptions of the question, the net force on the woman would be
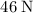 due west.
due west.
The acceleration of this
 woman would be:
woman would be:
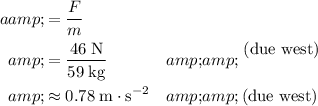 .
.