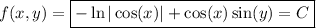The differential equation
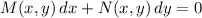
is considered exact if
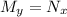 (where subscripts denote partial derivatives). If it is exact, then its general solution is an implicit function
(where subscripts denote partial derivatives). If it is exact, then its general solution is an implicit function
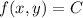 such that
such that
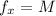 and
and
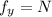 .
.
We have
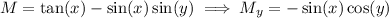

and
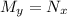 , so the equation is indeed exact.
, so the equation is indeed exact.
Now, the solution
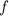 satisfies
satisfies
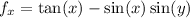
Integrating with respect to
 , we get
, we get
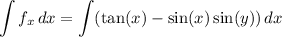
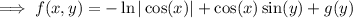
and differentiating with respect to
 , we get
, we get
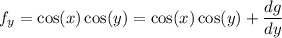
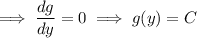
Then the general solution to the exact equation is