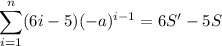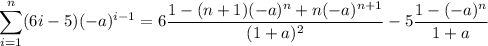Notice that the difference in the absolute values of consecutive coefficients is constant:
|-7| - 1 = 6
13 - |-7| = 6
|-19| - 13 = 6
and so on. This means the coefficients in the given series

occur in arithmetic progression; in particular, we have first value
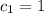 and for
and for
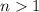 ,
,
 . Solving this recurrence, we end up with
. Solving this recurrence, we end up with
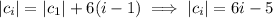
So, the sum to
 terms of this series is
terms of this series is
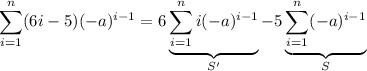
The second sum
 is a standard geometric series, which is easy to compute:
is a standard geometric series, which is easy to compute:
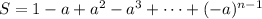
Multiply both sides by
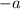 :
:

Subtract this from
 to eliminate the intermediate terms to end up with
to eliminate the intermediate terms to end up with
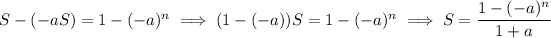
The first sum
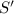 can be handled with simple algebraic manipulation.
can be handled with simple algebraic manipulation.
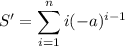
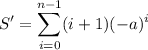
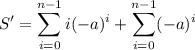
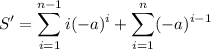
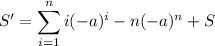
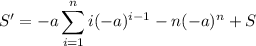
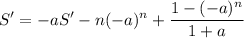

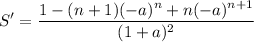
Putting everything together, we have