Question

Determine the equation of the tangent line in both cases

1. x^2/x+2 at (2,1)


2. x^3+2y^2=10y at (2,1)

Answer 1

Differentiate the function/equation with respect to x and solve for the derivative, dy/dx. The value of dy/dx at the given point is the slope of the tangent line to the curve at that point. Then use the point-slope formula to get the equation of the tangent.

1.

`y = (x^2)/(x+2) \implies (dy)/(dx) = (2x*(x+2) - x*1)/((x+2)^2) = (x(x+4))/((x+2)^2)`

When x = 2, the derivative is

`(dy)/(dx)\bigg|_(x=2) = (2(2+4))/((2+2)^2) = \frac34`

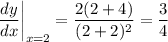
Then the equation of the tangent line at (2, 1) is

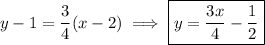
`y - 1 = \frac34 (x - 2) \implies \boxed{y = \frac{3x}4 - \frac12}`

2.

`x^3 + 2y^2 = 10y \implies 3x^2 + 4y (dy)/(dx) = 10 (dy)/(dx) \implies (dy)/(dx) = (3x^2)/(10-4y)`

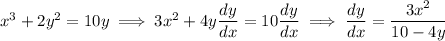
When x = 2 and y = 1, the derivative is

`(dy)/(dx)\bigg|_((x,y)=(2,1)) = (3*2^2)/(10-4*1) = 2`

Then the tangent at (2, 1) has equation

`y - 1 = 2 (x - 2) \implies \boxed{y = 2x - 3}`