Question

A principal of 2000 is invested at 3.25% interest, compounded annually. How much will the investment be worth after 10 years?

Answer 1

$2,753.79

Explanation:

Compound Interest Formula

`\large \text{$ \sf A=P\left(1+(r)/(n)\right)^(nt) $}`

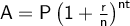
where:

• A = final amount
• P = principal amount
• r = interest rate (in decimal form)
• n = number of times interest applied per time period
• t = number of time periods elapsed

Given:

• P = $2,000
• r = 3.25% = 0.0325
• n = 1
• t = 10

Substitute the given values into the formula and solve for A:

`\implies \sf A=2000\left(1+(0.0325)/(1)\right)^((1 * 10))`

`\implies \sf A=2000(1.0325)^(10)`

`\implies \sf A=2753.788608...`

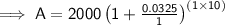
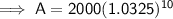
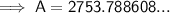
Therefore, the value of the investment after 10 years will be $2,753.79 to the nearest cent.