Question

PLEASE HELP!!! A system of linear equations is shown below.

2x –3y=17 –3x + y = –1 Choose a method (Elimination or Substitution) to solve the system of equations. Solve and explain your process. Academic Language: Elimination, Substitution, Graphing, Intersection, Solution, Coordinate Point, Ordered Pair, Solve, Isolate, Systems, Equations, Additive Inverse, Multiplicative Inverse, Distributive Property, Variable, Combine Like Terms, and Justify.

Answer 1

The value of the variable x is -2 and the value of the variable y is -7.

Explanation:

The substitution method consists of:

1. Solve for an unknown in one of the equations, which will be a function of the other unknown .
2. In the other equation that is not used, the same unknown is replaced by the expression obtained in step 1.
3. Solve for the only remaining unknown, obtaining the numerical value of an unknown.
4. Substitute the cleared unknown in step 3 for its numerical value in the equation obtained in step 1.
5. Operate to obtain the numerical value of the other unknown.

In this case, you have the system of equations:

`\left \{ {{2*x-3*y=17} \atop {-3*x+y=-1}} \right.`

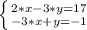
Isolating the variable y from the second equation:

y= -1 +3*x

Replacing this expression in the first equation:

2*x-3*( -1 +3*x)= 17

Solving:

2*x -3*(-1)-3*3*x= 17

2*x +3 -9*x= 17

2*x -9*x= 17 -3

(-7)*x= 14

x= 14÷(-7)

x= -2

Now, replacing the value of x in the expression y = -1 + 3 * x you get:

y= -1 +3*(-2)

Solving:

y= -1 -6

y= -7

So, the value of the variable x is -2 and the value of the variable y is -7.