More plainly, the sequence is defined recursively by
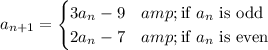
and some starting value
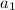 .
.
We're given that the sequence alternates between two constants,
 and
and
 , so that
, so that
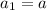 .
.
• If
 is even, then the second term
is even, then the second term
 must be odd, since
must be odd, since
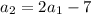
by the given rule, and 2×(even) - (odd) = (odd). So
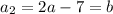
In turn, the third term is even, since we jump back to
 . From the given rule,
. From the given rule,

and so
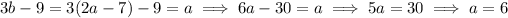

Then the sum of the two integers is

• You end up with the same answer in the case of odd
 , so I'll omit this part of the solution. (It's almost identical as the even case.)
, so I'll omit this part of the solution. (It's almost identical as the even case.)