Answer:
The true estimate of the average annual income of all 700 families living in a four square block section lies within the 92% confidence interval below

Explanation:
From the question we are told that
The sample size is n = 50
The sample mean is
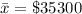
The population standard deviation is
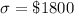
From the question we are told the confidence level is 92% , hence the level of significance is

=>
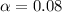
Generally from the normal distribution table the critical value of
 is
is
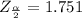
Generally the margin of error is mathematically represented as
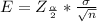
=>
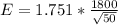
=>
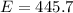
Generally 92% confidence interval is mathematically represented as
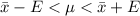
=>
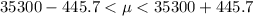
=>

So the true estimate of the average annual income of all 700 families living in a four square block section lies within the 92% confidence interval