Question

In a Harris poll of 514 human resource professionals, 90% said that the appearance of a job applicant is most important for a good first impression. Construct a 95% confidence interval for the proportion of all human resource professionals believing that the appearance of a job applicant is most important for a good first impression. Also find the margin of error. Round your answers to four decimal places.

Answer 1

Answer: The interval is 0.9 ± 0.0259 and margin of error is 0.0259

Explanation: Confidence interval for a proportion in one sample is the estimate of the proportion of a population. It is calculated following the next steps:

1) Find the proportion
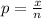`p=(x)/(n)`, in which x is the number of people with the desired condition. In our case, p=0.9;

2) Calculate margin of error, i.e.:

`z\sqrt{(p(1-p))/(n)}`

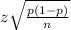
z is z-score, which for a 95% confidence, equals 1.96;

Substituting with the data given:

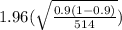`1.96(\sqrt{(0.9(1-0.9))/(514)})` = 0.0259

3) Write: p ±
`z\sqrt{(p(1-p))/(n)}`

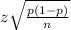
In our case, the interval will be 0.9 ± 0.0259.

Margin of error is the random sampling error in the results of a survey, i.e.,it shows you how far your result will be from the real value. For the Harris poll, margin of error is 0.0259