Question

2.
Determine if the function is Odd Even Neither.
[6]
f(x) = -3x4 + 2x3 – 5x2 + x

Answer 1

neither

Explanation:

• If f(x) = f(- x) then f(x) is even

• If f(- x) = - f(x) then f(x) is odd

Given

f(x) = - 3
`x^(4)` + 2x³ - 5x² + x , then

f(- x) = - 3
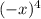`(-x)^(4)` + 2(- x)³ - 5(- x)² + (- x) = - 3
`x^(4)` - 2x³ - 5x² - x

Since f(x) ≠ f(- x) then f(x) is not Even

- f(x) = - (- 3
`x^(4)` + 2x³ - 5x² + x) = 3
`x^(4)` - 2x³ + 5x² - x

Since f(- x) ≠ - f(x) then f(x) is not Odd

Thus f(x) is neither even nor odd