Question

Hii! would anyone mind helping me out?

Find the center of this hyperbola


`\large\boldsymbol{9x^2-y^2-72x+8y+119=0}`


`\bigstar`


`\underbrace`

Answer 1

(4, 4)

Explanation:

This is the form of a hyperbola. Use this form to determine the values used to find vertices and asymptotes of the hyperbola.

`((x-h)^2)/(a^2) - ((y-k)^2)/(b^2) = 1`

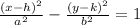
Match the values in this hyperbola to those of the standard form. The variable h represents the x-offset from the origin, k represents the y-offset from origin, a.

a = 1

b = 3

k = 4

h = 4

Thus,

`(x-4)^2 - ((y-4)^2)/(9) = 1`

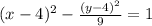
The center of a hyperbola follows the form of (h, k). Substitute in the values of h and k.

= (4, 4)