Question

A calorimeter contains 72.0 g of water at 19.2 oC. A 141 g piece of metal is heated to 89.0 oC and dropped into the water. The entire system eventually reaches 25.5 oC . What is the specific heat of the metal?

Answer 1

The specific heat of the metal is 0.212 J/(g°C).

Step-by-step explanation:

We can calculate the specific heat of the metal by the following equilibrium:

`q_(a) = -q_(b)`

`m_(a)C_(a)\Delta T_(a) = -m_(b)C_(b)\Delta T_(b)`

`m_(a)C_(a)(T_{f_(a)} - T_{i_(a)}) = -m_(b)C_(b)(T_{f_(b)} - T_{i_(b)})`

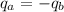
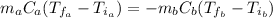
In the above equation, we have that the heat loses by the metal (b) is gained by the water (a).

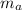`m_(a)`: is the water's mass = 72.0 g

`C_(a)`: is the specific heat of water = 4.184 J/(g°C)

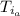`T_{i_(a)}`: is the initial temperature of the water = 19.2 °C

`T_{f_(a)}`: is the final temperature of the water = 25.5 °C

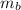`m_(b)`: is the metal's mass = 141 g

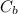`C_(b)`: is the specific heat of metal =?

`T_{i_(b)}`: is the initial temperature of the metal = 89.0 °C

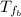`T_{f_(b)}`: is the final temperature of the water = 25.5 °C

`m_(a)C_(a)(T_{f_(a)} - T_{i_(a)}) = -m_(b)C_(b)(T_{f_(b)} - T_{i_(b)})`

`72.0 g*4.184 J/(g^(\circ) C)*(25.5 ^(\circ) C - 19.2 ^(\circ) C) = -141 g*C_(b)*(25.5 ^(\circ) C - 89.0 ^(\circ) C)`

`C_(b) = -(72.0 g*4.184 J/(g^(\circ) C)(25.5 ^(\circ) C - 19.2 ^(\circ) C))/(141 g(25.5 ^(\circ) C - 89.0 ^(\circ) C)) = 0.212 J/(g^(\circ) C)`

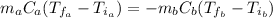
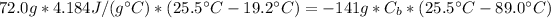
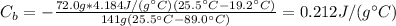
Therefore, the specific heat of the metal is 0.212 J/(g°C).

I hope it helps you!