Question

Suppose the waiting time in a Piggly Wiggly checkout line follows an Exponential distribution with an average wait of 7 minutes. What is the 80th percentile of waiting times?

Answer 1

Answer: 11.3 minutes

Explanation: Exponential Distribution is a distribution with function of the form:

`f(x)=\lambda.e^(-\lambda.x)`

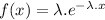
often related to an amount of time until an event occur.

The greek letter λ is decay parameter and have a relationship with the mean:

`\lambda=(1)/(\mu)`

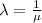
and x is the amount of time

Probability in exponential distribution is given by

`P(x<X)=1-e^(-\lambda.x)`

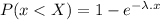
Percentile is a value below which a percentage of the data falls.

For the waiting line in a Piggly Wiggly checkout, 80th percentile will be

`P(x<h)=0.8`

`P(x<h)=1-e^{-(1)/(7)h}`

`0.8=1-e^{-(1)/(7)h}`

`e^{-(h)/(7) }=0.2`

`-(h)/(7) =ln(0.2)`

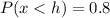
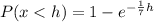
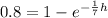
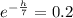
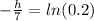
h = 11.3

The 80th percentile of waiting times is 11.3 minutes.