Complete Question
The National Appliance Company makes refrigerators. One of its suppliers, the Exeter company, produces plastic shelves for the refrigerators and ships them in large lots. The National Appliance Company requires that the percentage of the plastic shelves that are defective be no more than 10%. If more than 10% are defective, the Prime Factor Company will reject the lot. To test this, the National Appliance Company randomly selects 573 of the shelves and has them inspected. It turns out that 70 are defective. Use this information and a 5% level of significance to determine if National Appliance should reject the batch.
Answer:
The decision rule is
Reject the null hypothesis
The conclusion is
There is no sufficient evidence to conclude that proportion of defective shelf is less than or equal to 0.10 hence the National Appliance Company should reject that batch of shelfs
Explanation:
From the question we are told that
The population of defective plastics is
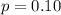
The sample size is n = 573
The number of shelf that are defective is k = 70
The level of significance is

Generally the sample proportion is mathematically represented as
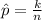
=>
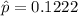
The null hypothesis is

The alternative hypothesis is

Generally the test statistics is mathematically represented as
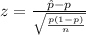
=>

=>
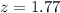
From the z table the area under the normal curve to the right corresponding to 1.77 is
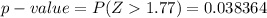
From the question we are told that
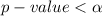 hence
hence
The decision rule is
Reject the null hypothesis
The conclusion is
There is no sufficient evidence to conclude that proportion of defective shelf is less than or equal to 0.10 hence the company should reject theat batch of shelfs