Question

The axis of a circular cylinder coincides with the z-axis and it rotates with an angular velocity of (3i−5j +9k) rad/s. Determine i. The tangential velocity at a point P on the cylinder, whose co-ordinates are ( j +5k) metres,

Answer 1

The tangential velocity at point P is
`\vec v_(P) = -34\,\hat{i} -15\,\hat{j}+3\,\hat{k}\,\,\left[(m)/(s) \right]`.

Step-by-step explanation:

Vectorially speaking, we define tangential velocity at point P (
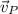`\vec v_(P)`), measured in meters per second, by the following vectorial expression:

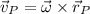`\vec v_(P) = \vec \omega * \vec r_(P)` (1)

Where:

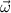`\vec \omega` - Angular velocity of the cylinder, measured in radians per second.

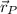`\vec r_(P)` - Radius of rotation, measured in meters.

If we know that
`\vec \omega = 3\,\hat{i}-5\,\hat{j}+9\,\hat{k}\,\left[(rad)/(s) \right]` and
`\vec r_(P) = \hat{j}+5\,\hat{k}\,[m]`, then the tangential velocity at point P is:

`\vec v_(P) = \left|\begin{array}{ccc}\hat{i}&\hat{j}&\hat{k}\\3\,(rad)/(s) &-5\,(rad)/(s) &9\,(rad)/(s) \\0\,m&1\,m&5\,m\end{array}\right|`

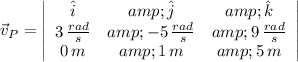
`\vec v_(P) = \left[\left(-5\,(rad)/(s) \right)\cdot (5\,m)-(1\,m)\cdot \left(9\,(rad)/(s) \right)\right]\,\hat{i}-(5\,m)\cdot \left(3\,(rad)/(s)\right)\,j +\left(3\,(rad)/(s) \right)\cdot (1\,m)\,\hat{k}`

`\vec v_(P) = -34\,\hat{i} -15\,\hat{j}+3\,\hat{k}\,\,\left[(m)/(s) \right]`

The tangential velocity at point P is
`\vec v_(P) = -34\,\hat{i} -15\,\hat{j}+3\,\hat{k}\,\,\left[(m)/(s) \right]`.