Given :-
- PQ = 8cm
- Radius = 5cm
- Two Tangents = P & Q.
Construction :-
⟼ Solution :-
Here, ΔTPQ is isosceles and TO is the angle bisector of ∠PTO.
[∵ TP=TQ = Tangents from T upon the circle]
⠀⠀⠀⠀⠀⠀⠀⠀∴ OT⊥PQ
⠀⠀⠀
___________________________________________
 By Applying Pythagoras Theorem in ∆OPR :
By Applying Pythagoras Theorem in ∆OPR :
OR = √OP² - PR²
OR = √5² - 4²
OR = 3cm
__________________________________________
Now,
 ∠TPR + ∠RPO = 90° (∵TPO=90°)
∠TPR + ∠RPO = 90° (∵TPO=90°)
 ∠TPR + ∠PTR (∵TRP=90°)
∠TPR + ∠PTR (∵TRP=90°)
 ∴ ∠RPO = ∠PTR
∴ ∠RPO = ∠PTR
⠀⠀
∴ Right triangle TRP is similar to the right triangle PRO. [By A-A Rule of similar triangles]
⟼
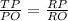
⟼
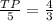
⟼
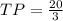
Hence you got your answer here.
⠀⠀⠀⠀⠀
-MissAbhi