Question

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. the length TP in cm is: ​

Answer 1

Given :-

• PQ = 8cm
• Radius = 5cm
• Two Tangents = P & Q.

Construction :-

• Join OT.

⟼ Solution :-

Here, ΔTPQ is isosceles and TO is the angle bisector of ∠PTO.

[∵ TP=TQ = Tangents from T upon the circle]

⠀⠀⠀⠀⠀⠀⠀⠀∴ OT⊥PQ

• So, PR = RQ = 4cm.

⠀⠀⠀

___________________________________________

`\longmapsto{}`By Applying Pythagoras Theorem in ∆OPR :

OR = √OP² - PR²

OR = √5² - 4²

OR = 3cm

__________________________________________

Now,

`\leadsto`∠TPR + ∠RPO = 90° (∵TPO=90°)

`\leadsto`∠TPR + ∠PTR (∵TRP=90°)

`\leadsto`∴ ∠RPO = ∠PTR

⠀⠀

∴ Right triangle TRP is similar to the right triangle PRO. [By A-A Rule of similar triangles]

⟼
`(TP)/(PO) = (RP)/(RO)`

⟼
`(TP)/(5) = (4)/(3)`

⟼
`TP= (20)/(3)`

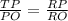
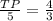
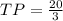
Hence you got your answer here.

⠀⠀⠀⠀⠀

-MissAbhi