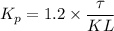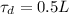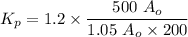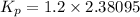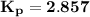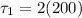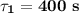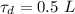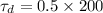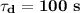Question

Determine the settings of KP, TI and TD required for a three-mode controller which gave a process reaction curve with a lag L of 200 s and a gradient R of 0.010%/s when the test signal was a 5% change in the control valve position.

Answer 1

`\mathbf{K_p =2.857}`

`\mathbf{\tau_1= 400 \ s}`

`\mathbf{ \tau_d = 100 \ s}`

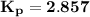
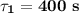
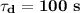
Step-by-step explanation:

We can determine each parameter by using the first method of Zeigler Nichols

`K_p = 1.2 * (\tau)/(KL)`

`\tau_1= 2L`

`\tau_d = 0.5 L`

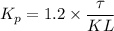
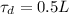
For this process;

the initial state of the output =
`A_o`

`\tau = constant`

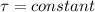
For calculating the gradient, we use the equation:

`y-y_o = G(t-t_o) \\ \\ y-A_o = 0.01 \% A_o (t-L)`

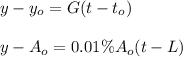
where.

Time constant relates to the time
`y = K = 1.05 A_o`

∴

`1.05A_o -A_o = 0.01\% A_o (t-200)`

`0.05 A_o = 0.0001 A_o (t-200)`

`t = 500A_o + 200`

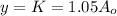
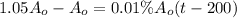
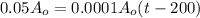
To find time t

`\tau = (500A_o +200) -200`

`\tau = 500 \ A_o`

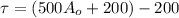
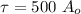
Recall that:

Using the first method of Zeigler Nichols

`K_p = 1.2 * (\tau)/(KL)`

`\tau_1= 2L`

`\tau_d = 0.5 L`

`K_p = 1.2 * (500 \ A_o)/(1.05\ A_o * 200)`

`K_p = 1.2 * 2.38095`

`\mathbf{K_p =2.857}`

`\tau_1= 2L`

`\tau_1= 2(200)`

`\mathbf{\tau_1= 400 \ s}`

`\tau_d = 0.5 \ L`

`\tau_d = 0.5 * 200`

`\mathbf{ \tau_d = 100 \ s}`