Answer:
657 pounds
Explanation:
Given
Represent the amount of fertilizer with x and the yield with y.
So, we have:
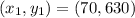
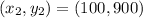
Required:
Determine the yield (y) when fertilizer (x) is 73ft^3
Using linear interpolation, we have:
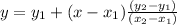
Substitute the x and y values using
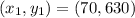 and
and
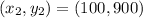 ;
;
We have:
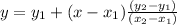
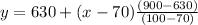
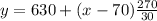
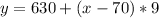
Open bracket
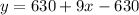
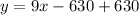
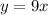
To solve for y when x = 73.
We simply substitute 73 for x
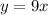
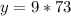
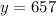
Hence, the yield for 73 cubic feet is 657 pounds