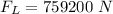Answer:
The value is
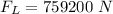
Step-by-step explanation:
From the question we are told that
The speed of air across the top of its wings is
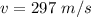
The speed of air below its wings is
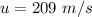
The density of air is
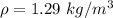
The area of the wing is
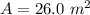
Generally the lifting force is mathematically represented as

Here
 is the difference in kinetic energy density between the top and the bottom
is the difference in kinetic energy density between the top and the bottom
![\Delta P = (1)/(2) * \rho * [v^2 - u^2 ]](https://img.qammunity.org/2021/formulas/physics/college/a15wfd50jwcrdsgpz5scdz6st0unw58dly.png)
=>
![\Delta P = (1)/(2) * 1.29 * [297^2 - 209^2 ]](https://img.qammunity.org/2021/formulas/physics/college/kqx9dcan6pds2f5htj5nocqqbkn7x0c05t.png)
=>
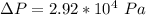
So

=>