Answer:
y-coordinate is decreasing at the rate of
 unit/sec.
unit/sec.
Explanation:
Given that:
The curve of the particle
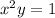
Then:
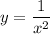
Taking the differential of y with respect to t
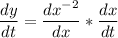
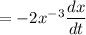
At (2, 1/4)
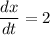
This implies that:
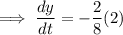
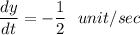
Thus, y-coordinate is decreasing at the rate of
 unit/sec.
unit/sec.