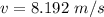Answer:
The value speed is
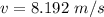
Step-by-step explanation:
From the question we are told that
The mass of the ping pong ball is
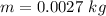
The radius is
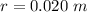
The depth of the ping pong inside the water is
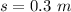
Gnerally the force with which the ball will emerge will from the water is mathematically represented as
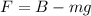
Here B is the Buoyant force on the ball which is mathematically represented as
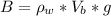
Here
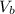 is the volume of the ball which is mathematically represented as
is the volume of the ball which is mathematically represented as
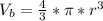
=>

=>
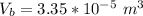
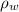 is the density of water with value
is the density of water with value
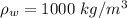
So
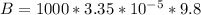
=>
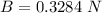
So
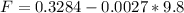
=>
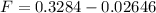
=>
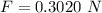
Generally force is mathematically represented as
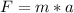
So
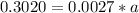
=>
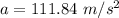
Generally from kinematic equation
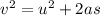
Here u is the velocity of the ping pong at depth of 0.3 m and the value is zero given that at that point there was no motion
So

=>