Answer:
(4, 4)
Explanation:
This is the form of a hyperbola. Use this form to determine the values used to find vertices and asymptotes of the hyperbola.

Match the values in this hyperbola to those of the standard form. The variable h represents the x-offset from the origin, k represents the y-offset from origin, a.
a = 1
b = 3
k = 4
h = 4
Thus,
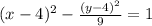
The center of a hyperbola follows the form of (h, k). Substitute in the values of h and k.
= (4, 4)