Question

Suppose that 4 ≤ f '(x) ≤ 5 for all values of x. What are the minimum and maximum possible values of f(4) − f(2)? ______≤ f(4) − f(2) ≤ ______

Answer 1

`8 \le f(4) - f(2) \le 10`

Explanation:

Given

`4 \le f'(x) \le 5`

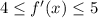
Required

Determine the minimum and maximum value of f(4) - f(2)

This question will be answered using the following mean value theorem.

`f'(x) = (f(b) - f(a))/(b - a)`

In this case:
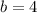`b = 4` and
`a = 2`

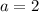
So, we have:

`f'(x) = (f(4) - f(2))/(4 - 2)`

`f'(x) = (f(4) - f(2))/(2)`

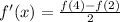
Make f(4) - f(2), the subject:

`f(4) -f(2) = 2 * f'(x)`

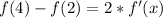
From the given range:
`4 \le f'(x) \le 5`

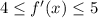
We have that; f'(x) is at minimum at 4

So, the minimum of f(4) - f(2) is:

`f(4) -f(2) = 2 * 4`

`f(4) -f(2) = 8`

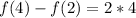
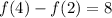
We have that; f'(x) is at maximum at 5

So, the maximum of f(4) - f(2) is:

`f(4) - f(2) = 2 * 5`

`f(4) - f(2) = 10`

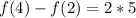
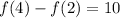
Hence, the minimum and maximum values can be expressed as:

`8 \le f(4) - f(2) \le 10`