Given:
A line through the points (7,1,-5) and (3,4,-2).
To find:
The parametric equations of the line.
Solution:
Direction vector for the points (7,1,-5) and (3,4,-2) is
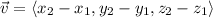
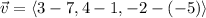
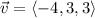
Now, the perimetric equations for initial point
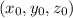 with direction vector
with direction vector
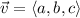 , are
, are

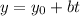
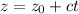
The initial point is (7,1,-5) and direction vector is
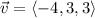 . So the perimetric equations are
. So the perimetric equations are
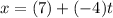
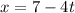
Similarly,
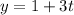
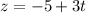
Therefore, the required perimetric equations are
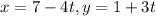 and
and
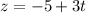 .
.