Question

The acceleration of a particle is defined by the relation a= -k/x. It has been experimentally determined that v=15 ft/s when x=0.6 ft and that v=9 ft/s when x=1.2 ft. Determine (a) velocity of particle when x=1.5 ft.(b)Position of particle at which velocity is zero.

Answer 1

(a) 5.89 ft/s

(b) x= 1.77 ft

Step-by-step explanation:

Given that the acceleration of the particle, a=-k/x

As
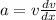`a=v(dv)/(dx)` , so

`v(dv)/(dx)=-(k)/(x) \\\\\Rightarrow vdv=-k(dx)/(x) \\\\`

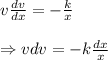
On integrating both sides, we have

`(v^2)/(2)=-k\ln(x) + C\cdots(i)`

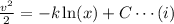
where C is a constant.

At x=0.6 ft, v=15 ft/s

From equation (i)

`(15^2)/(2)=-k\ln(0.6) + C \\\\\Rightarrow C=(225)/(2) + k\ln(0.6) \cdots(ii)`

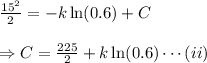
Similarly, at x=1.2 ft, v=9 ft/s

`(9^2)/(2)=-k\ln(1.2) + C \\\\\Rightarrow (81)/(2) = -k\ln(1.2) + (225)/(2) + k\ln(0.6) \\\\\Rightarrow k(\ln(1.2) - \ln(0.6))= (225)/(2)-(81)/(2) \\\\\Rightarrow k\ln(1.2/0.6)= 72 \\\\\Rightarrow k = 72 / ln(2)=103.87`

From equation (ii),

`C=(225)/(2) + 103.87 * \ln(0.6) \\\\\Rightarrow C=112.5-53.06=59.44`

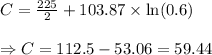
Putting the value of k and C in the equation (i), we have

`(v^2)/(2)=-103.87\ln(x) + 59.44 \\\\\Rightarrow v^2=-207.74\ln(x) + 118.88 \\\\\Rightarrow v = √(-207.74\ln(x) + 118.88)`

(a) At x=1.5 ft, the velocity of the particle is

`\Rightarrow v = √(-207.74\ln(1.5) + 118.88) \\\\`

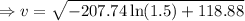
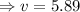`\Rightarrow v = 5.89` ft/s

At x=1.5 ft, the velocity of the particle is 5.89 ft/s.

(b) For v=0, we have

`\Rightarrow 0 = √(-207.74\ln(x) + 118.88) \\\\\Rightarrow \ln(x) = -118.88/-207.74=0.572 \\\\\Rightarrow x= e^(0.572) \\\\`

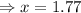`\Rightarrow x= 1.77` ft

At x= 1.77 ft the velocity of the particle is zero.