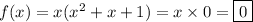Since
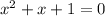 means
means
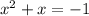 , we have for any
, we have for any
 the recursive relation
the recursive relation
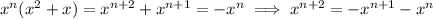
Let
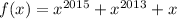 . Substitution using the recursive rule generates an alternating power-reduction pattern:
. Substitution using the recursive rule generates an alternating power-reduction pattern:

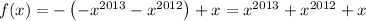
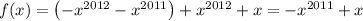
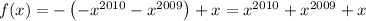
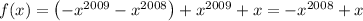
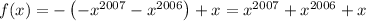
and so on.
Notice that in the equivalent forms of
 involving 3 terms, the largest power of
involving 3 terms, the largest power of
 is a multiple of 3, and the next largest power is 1 less. This means after so many iterations of substitutions, we would end up with
is a multiple of 3, and the next largest power is 1 less. This means after so many iterations of substitutions, we would end up with
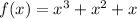
Then by factorizing, the expression of interest reduces to