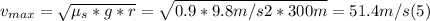Question

What is the maximum speed your car can go around a flat 300m radius turn. Assume a coefficient of static friction of 0.9.

Answer 1

vmax = 51.4 m/s

Step-by-step explanation:

• If the turn is flat, this means that the car is not accelerated in the vertical direction, so the normal force and the force of gravity are equal each other in magnitude, as follows:

`F_(n) = F_(g) = m*g (1)`

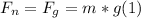
• At the same time there exists a single force that keeps the car turning, which is the centripetal force, aiming to the center of the turn.
• This force is not a different force, is just the net force acting on the car in the horizontal direction, which is the friction force.
• This friction reaches to a maximum value, when the friction force is equal to the static friction force.
• This force can be expressed as follows:

`F_(fs) = \mu_(s) *F_(n) = \mu_(s) * m*g (2)`

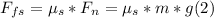
• This force must be equal to the maximum centripetal force, which can be written as follows:

`F_(c) = m*(v^(2))/(r) (3)`

• Since the left sides of (2) and (3) are equal each other, right sides must be equal too:

`\mu_(s) * m*g = m*(v^(2))/(r) (4)`

• Rearranging, and solving for v, we get the maximum speed that the car can go around the turn without sliding:

`v_(max) =\sqrt{\mu_(s) *g*r} =√(0.9*9.8m/s2*300m) = 51.4 m/s (5)`