Question

Pls help meeeee I only have 5 mins left use the graph from number 3 to anwser number 4

Answer 1

Option C

Explanation:

From the graph attached,

Slope of the line passing through two points A and B will be,

m =
`\frac{\text{Rise}}{\text{Run}}`

=
`(12)/(8)`

=
`(3)/(2)`

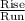
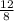
Triangles having same ratio of Height and base (slope) will lie on the line graphed.

Option A

Slope pf the triangle =
`(44)/(21)`

`(3)/(2)\\eq (44)/(21)`

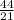
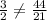
Slope of the line ≠ Slope of the triangle

Therefore, triangle will not lie on the line.

Option B

Slope of the triangle =
`(36)/(12)=(3)/(1)`

`(3)/(2)\\eq (3)/(1)`

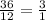
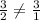
Triangle will not lie on the line.

Option C

Slope of the triangle =
`(30)/(20)= (3)/(2)`

Since, slope of the line = slope of the triangle

`(3)/(2)= (3)/(2)`

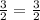
Triangle will lie on the line.

Option D

Slope of the triangle =
`(52)/(26)=(2)/(1)`

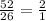
But
`(3)/(2)\\eq (2)/(1)`

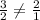
Therefore, triangle will not lie on the given line.