Given:
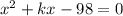
One of the two roots of the given equation is double the additive inverse of the other.
To find:
The value of k.
Solution:
Let two roots of the given equation are
 and
and
 .
.
According to the question,
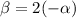 (Additive inverse of
(Additive inverse of
 is
is
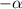 )
)
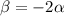
If
 and
and
 are roots of the quadratic equation
are roots of the quadratic equation
 then
then
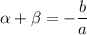
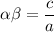
We have,
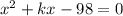
Here, a =1, b=k and c=-98.

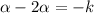
![[\because \beta=-2\alpha]](https://img.qammunity.org/2021/formulas/mathematics/high-school/c0b5ek8ivxtfxkvp67fdfs733loe3mj0ko.png)
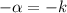
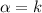 ...(i)
...(i)
Now,
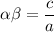
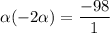
![[\because \beta=-2\alpha]](https://img.qammunity.org/2021/formulas/mathematics/high-school/c0b5ek8ivxtfxkvp67fdfs733loe3mj0ko.png)
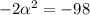
Divide both sides by -2.
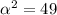
Taking square root on both sides.
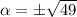
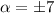
Using (i), we get
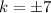
Therefore, the value of k is either -1 or 1.