Question

What is an equation of the line that passes through the points (-6, -2) and

(-3, 2)? Put your answer in fully reduced form.

Answer 1

The equation of line is:
`\mathbf{4x-3y=-18}`

Explanation:

We need to find an equation of the line that passes through the points (-6, -2) and (-3, 2)?

The equation of line in slope-intercept form is:
`y=mx+b`

where m is slope and b is y-intercept.

We need to find slope and y-intercept.

Finding Slope

Slope can be found using formula:
`Slope=(y_2-y_1)/(x_2-x_1)`

We have
`x_1=-6,y_1=-2, x_2=-3, y_2=2`

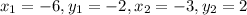
Putting values and finding slope

`Slope=(2-(-2))/(-3-(-6))\\Slope=(2+2)/(-3+6) \\Slope=(4)/(3)`

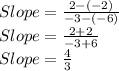
So, we get slope:
`m=(4)/(3)`

Finding y-intercept

Using point (-6,-2) and slope
`m=(4)/(3)` we can find y-intercept

`y=mx+b\\-2=(4)/(3)(-6)+b\\-2=4(-2)+b\\-2=-8+b\\b=-2+8\\b=6`

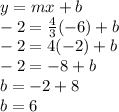
So, we get y-intercept b= 6

Equation of required line

The equation of required line having slope
`m=(4)/(3)` and y-intercept b = 6 is

`y=mx+b\\y=(4)/(3)x+6`

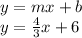
Now transforming in fully reduced form:

`y=(4x+6*3)/(3) \\y=(4x+18)/(3) \\3y=4x+18\\4x-3y=-18`

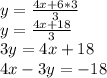
So, the equation of line is:
`\mathbf{4x-3y=-18}`