Answer:
The correct option is;
The graph has a vertical asymptote at x = -3
Explanation:
Whereby the given function is
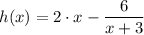 , we have;
, we have;
The function is undefined at x = -3, therefore, the function has a verical asymptote at x = -3
The graph crosses the x-axis (the x-intercept) when the y coordinate, value h(x) = 0, therefore, we have;
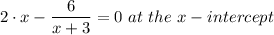
Which gives;
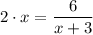
2·x² + 6·x - 6 = 0
Dividing by 2 gives;
x² + 3·x - 3 = 0
x = (-3 ± √(3² - 4×1×(-3)))/(2 × 1) = (-3 ± √21)/2
Similarly, the y-intercept occurs when h(0) = -2 as follows;
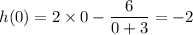
Therefore, the graph crosses the y-axis, the y-intercept at (0, -2)
The correct option is, that the graph has a vertical asymptote at x = -3