Answer:
x = 25
Explanation:
From the picture attached,
ΔABC and ΔADE are the similar triangles.
Therefore, their corresponding sides will be in the same ratio.
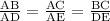
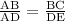
And AB = AD + DB
= 2(AD) [Since, AD = DB]
By substituting these values,
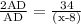
2 =
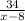
x - 8 =
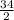
x - 8 = 17
x = 17 + 8
x = 25