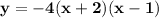Question

Please help !!! I have no idea what I’m doing and can’t find anyone to teach me this

Answer 1

The required equation in factored form is:
`\mathbf{y=-4(x+2)(x-1)}`

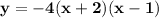
Explanation:

In this question we need to find the equation of the graph in factored form.

The factored form will be:
`f(x)=a(x-r_1)(x-r_2)..`

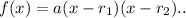
where a is y-intercept and r₁, r₂ are x-intercepts

X-intercepts

When y=0, the values of x axis are known as x-intercepts

Y-intercepts

When x=0, the values of y-axis are known as y-intercepts.

Looking at the graph finding x-intercepts

When y=0 x=-2 and 1

So, we have

r₁ = -2

r₂ = 1

Looking at the graph finding y-intercepts

When x=0, y=-4

So, a = -4

Putting values in the formula we will get:

`f(x)=a(x-r_1)(x-r_2)\\f(x)=-4(x-(-2))(x-1)\\f(x)=-4(x+2)(x-1)`

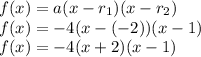
So, the required equation in factored form is:
`\mathbf{y=-4(x+2)(x-1)}`