Answer:
Triangle Z
Step-by-step explanation:
Required
Similar triangle to triangle C
Similar triangles do not necessarily have the same size. However, they must be in proportion of size and their angles must be equal.
From the list of options given, triangle Z is a dilation of C and this is shown below.
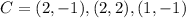
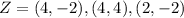
Divide the corresponding coordinates of Z by C to get the scale factor.
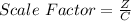
For
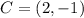 and
and

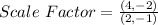
Factorize:

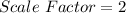
For
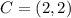 and
and
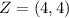
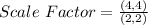
Factorize:
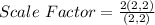
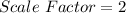
Lastly;
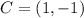
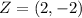
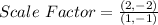
Factorize:

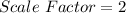
Notice that the scale factor is the same all through.
Hence, Z is similar to C