Question

Find x such that f(x) = 10 given f(x) = 4x+2

Answer 1

x=2

Explanation:

So you make the equation equal. f(x)=10 so you would put it as 10=4x+2, than you subtract two from both sides making it 8=4x and than divide both sides by 4 making it 2=x.

Answer 2

`\boxed {\boxed {\sf x=2}}`

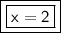
Explanation:

We know that:

`f(x)=4x+2 \\f(x)= 10`

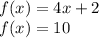
Both 4x+2 and 10 are equal to f(x). We can use substitution and set 4x+2 and 10 equal to each other.

`4x+2=10`

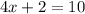
Now, solve for x. Perform the inverse operations to isolate x on one side of the equation.

2 is being added to 4x. The inverse of addition is subtraction. Subtract 2 from both sides of the equation.

`4x+2-2=10-2`

`4x=10-2 \\`

`4x=8`

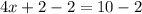
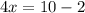
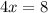
x is being multiplied by 4. The inverse of multiplication is division. Divide both sides of the equation by 4.

`(4x)/(4) =(8)/(4)`

`x=(8)/(4)`

`x=2`

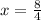
For the function f(x)= 4x+2, when f(x)=20, x=2