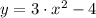Answer:
a) We kindly invite you to read the explanation and check the image attached below for further details.
b) The rectangular equation is
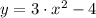 .
.
Step-by-step explanation:
a) Let
 and
and
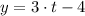 for
for
![t\in[0,4]](https://img.qammunity.org/2021/formulas/mathematics/college/tpngbq8y4ipse1nqsnsecw7qosrwoy2f0r.png) . We proceed to graph the expression with the help of a graphing tool. In this case, the tool Desmos is used and the result is presented below.
. We proceed to graph the expression with the help of a graphing tool. In this case, the tool Desmos is used and the result is presented below.
b) The rectangular equation for the curve is:
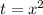 (1)
(1)
 (2)
(2)
By applying (1) in (2), we get the following equation in rectangular form: