Answer:
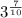 or
or
![\sqrt[10]{3^7}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wcuw1b5vweyyt6haq8zv902jjwq13zil69.png)
Explanation:
![\left(√(3)\right)\left(\sqrt[5]{3}\right)=\sqrt[10]{3^7}\quad](https://img.qammunity.org/2023/formulas/mathematics/high-school/bctvbpdarylozuno1pwmn09rec1uqf1otw.png)
(√3)(
![\sqrt[5]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1uat3iwmmsptsc262z10h3hmpmobv0epe3.png) ) = √3 ·
) = √3 ·
![\sqrt[5]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1uat3iwmmsptsc262z10h3hmpmobv0epe3.png)
{√3 =
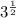 } {radical rule:
} {radical rule:
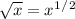 }
}
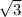
![\sqrt[5]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1uat3iwmmsptsc262z10h3hmpmobv0epe3.png) =
=
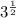 ·
·
![\sqrt[5]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1uat3iwmmsptsc262z10h3hmpmobv0epe3.png)
{
![\sqrt[5]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1uat3iwmmsptsc262z10h3hmpmobv0epe3.png) =
=
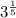 } {radical rule:
} {radical rule:
![\sqrt[n]{x} = x^1^/^n](https://img.qammunity.org/2023/formulas/mathematics/high-school/nikw7qmqgmnko4csrci4c01ctop7jidhfl.png) }
}
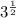 ·
·
![\sqrt[5]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1uat3iwmmsptsc262z10h3hmpmobv0epe3.png) =
=
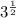 ·
·
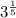 {exponent rule:
{exponent rule:
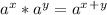 }
}
(1/2 + 1/5 = 5/10 + 2/10 = 7/10)
 {opposite of radical rule:
{opposite of radical rule:
![\sqrt[n]{x} = x^1^/^n](https://img.qammunity.org/2023/formulas/mathematics/high-school/nikw7qmqgmnko4csrci4c01ctop7jidhfl.png) ;
;
![x^(a)/(b)=\sqrt[b]{x^a}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ty3u12di826ggpk63xbx4g8lgevfps5bh9.png) }
}
=
![\sqrt[10]{3^7}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wcuw1b5vweyyt6haq8zv902jjwq13zil69.png)
so, the simplified version of this equation can either be written as:
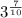 or
or
![\sqrt[10]{3^7}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wcuw1b5vweyyt6haq8zv902jjwq13zil69.png)
hope this helps!!
(I can't clearly see the last option, but if it's either of these, then it's correct)