Question

The Candle Factory is producing a new candle. It has a radius of 3 inches and a height of 5 inches. How much wax is needed to make the candle? Use 3.14 for Pi. Round to the nearest whole cubic inch.

A cylinder with a radius of 3 inches and height of 5 inches.

Recall the formulas S A = 2 pi r squared + 2 pi r h and V = pi r squared h.
141 cubic inches
236 cubic inches
443 cubic inches
565 cubic inches

Answer 1

141 cubic inches

Explanation:

The candle can be modeled as a cylinder.

To find how much wax is needed to make the candle, calculate the volume of the cylinder.

`\textsf{Volume of a cylinder}=\sf \pi r^2 h \quad\textsf{(where r is the radius and h is the height)}`

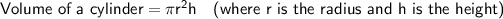
Given:

• r = 3 in
• h = 5 in
• π = 3.14

Substitute the given values into the formula and solve for V:

`\implies \sf V=3.14 \cdot 3^2 \cdot 5`

`\implies \sf V=3.14 \cdot 9 \cdot 5`

`\implies \sf V=28.26 \cdot 5`

`\implies \sf V=141.3\:in^3`

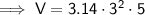
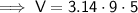
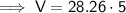
Therefore, the amount of wax needed to make the candle is 141 cubic inches (nearest whole cubic inch).