The solution to the system of equations is
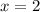 and
and
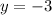 .
.
To find the solution of the system of equations, you can use the method of elimination. Add the two equations to eliminate the \(y\)-terms:
![\[ (2x + 5y) + (-8x - 5y) = -11 + (-1) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/hnz5z9q1shhxrfnippbpld36pckenv8lgn.png)
Combine like terms:
![\[ -6x = -12 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/n05bnyw96cq06mchu9xbyyjew5eaop2nzz.png)
Now, solve for \(x\):
![\[ x = (-12)/(-6) = 2 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/loo0bxji0i9o0q2tyfzmgdbyy354q87asw.png)
Now that you have the value of \(x\), substitute it back into one of the original equations to solve for \(y\). Let's use the first equation:
![\[ 2x + 5y = -11 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/2rngio80qi320eymfevvpxqe6ongbn9ulj.png)
![\[ 2(2) + 5y = -11 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/htc67ekorlufd08n5q831fk5c6fzvrrti2.png)
![\[ 4 + 5y = -11 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/p3josez6zrzzuzmrh9s18rwlelr6o4d0pm.png)
Subtract 4 from both sides:
![\[ 5y = -15 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/gnmmt3sqtpj9rwjduw5nwm2adx5ypqpxtq.png)
Divide by 5:
![\[ y = -3 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fzt0866q4dz6q9pnhiiqzdbagc8pk1a6qv.png)
So, the solution to the system of equations is
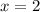 and
and
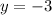 .
.